
回帰分析を使った予測を行いたいけど、思うような結果が出ないということはありませんか?
もしかしたらそれ、「データの形式」が回帰分析に適切ではないことが原因かもしれません。
例えば、データを時系列順に縦に並べてしまっている場合、それは時系列分析に適したデータになってしまします。正しい分析結果を出すには、分析手法に合った正しい形式のデータが必要です。
そこで今回は、回帰分析に適した正しいデータ形式を、もう一つの分析手法の「時系列分析」と、比較しながらご紹介します。
回帰分析をしてみたいけど、どんなデータの形、持ち方にすれば良いのかわからないという方も、こちら記事を参考にしていただければ幸いです。
回帰分析と時系列分析の違い
はじめに、回帰分析と時系列分析の違いをご紹介します。
1-1.回帰分析と時系列分析
数値を予測するための分析手法には回帰分析と時系列分析の2種類があります。
(1)回帰分析:事象Aが事象Bにどのような影響を及ぼしたかを関数の形で明らかにする分析手法
(2)時系列分析:現象の時間変動を分析し、将来の予測などを行なう分析手法
※2023年7月現在、Geminiotで扱えるのは回帰分析となります。 時系列分析は今後のバージョンアップにて実装を想定しております。
<回帰分析>
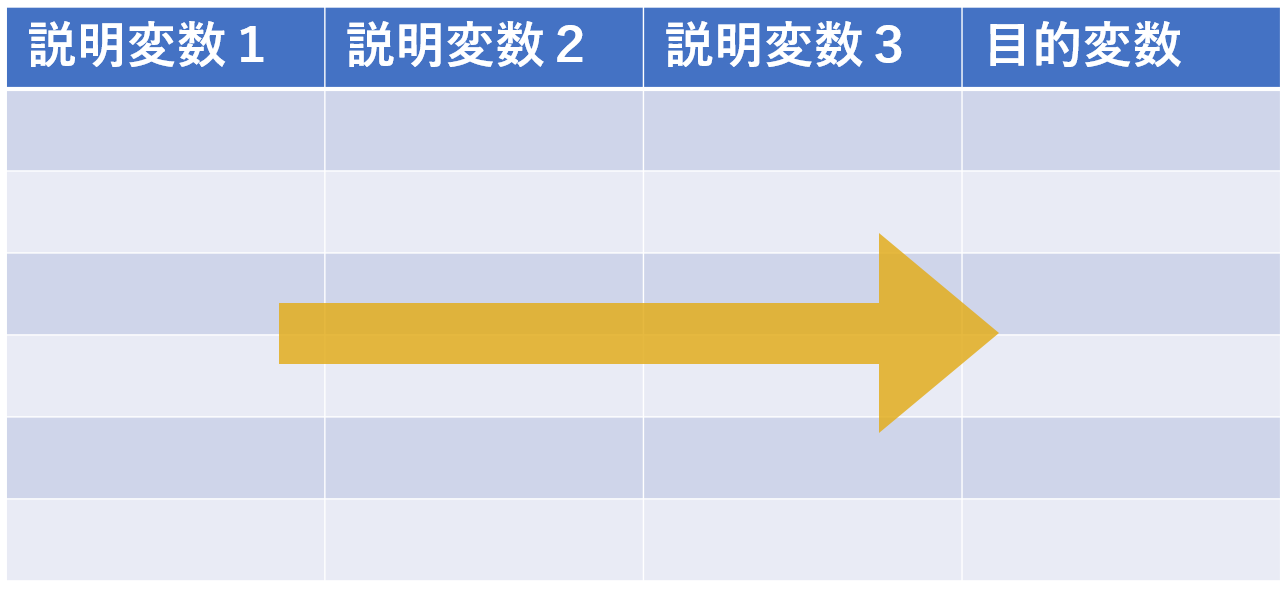
回帰は目的変数と他の変数と関係を学習するため、レコード毎に横方向に関係を確認していく。
(「目的変数」:求めたい要素、「説明変数」:求めたい要素に影響を与える要素)
<時系列分析>
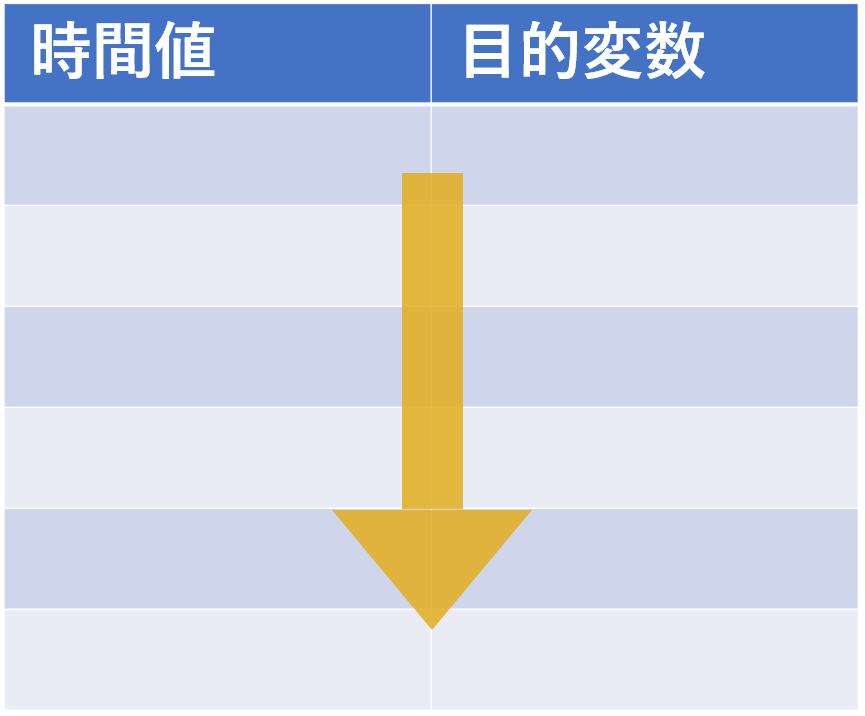
時系列は目的変数の過去から現在までの変化を学習するため、時系列順に縦方向に関係を確認していく。
1-2.回帰分析の学習イメージ
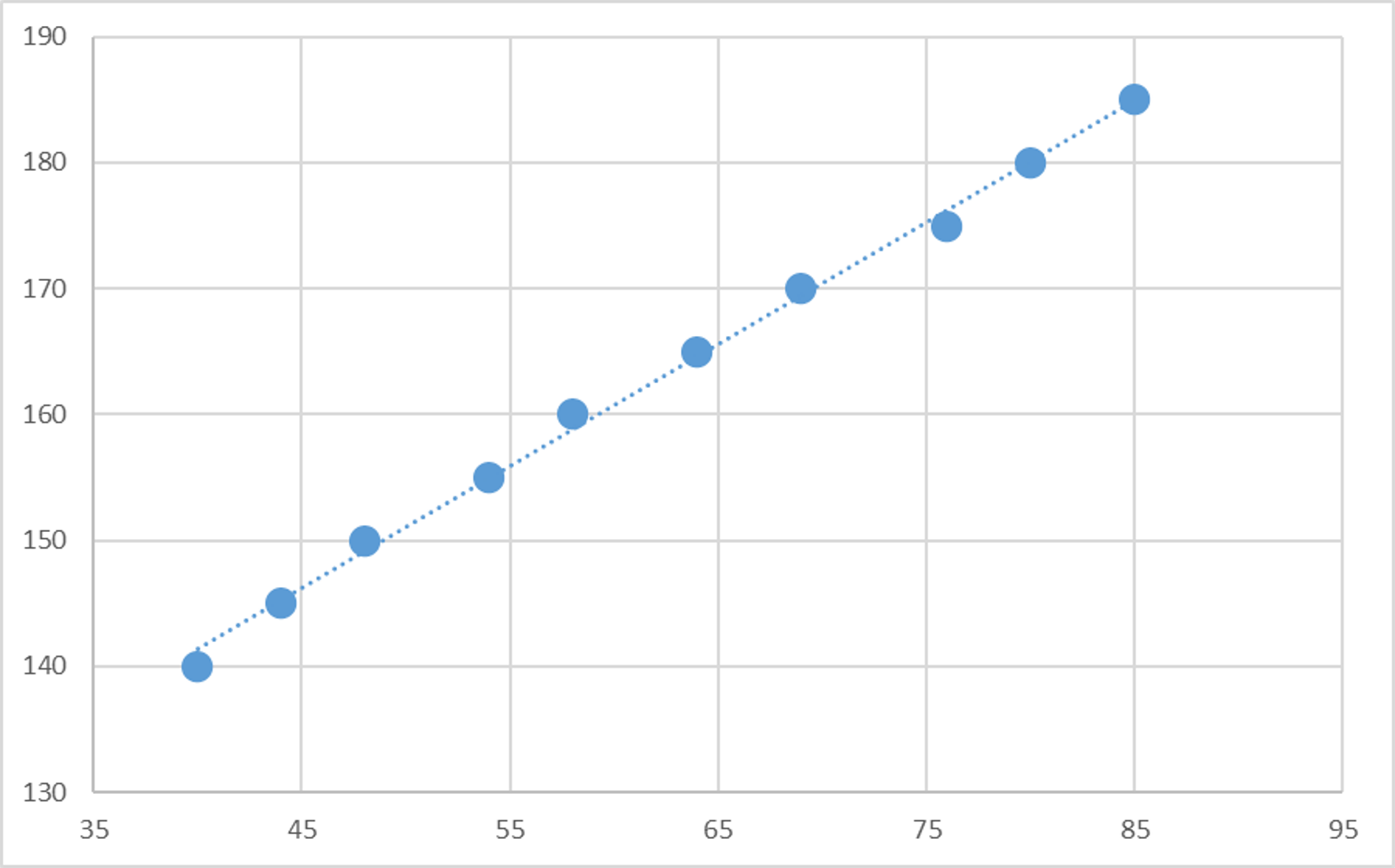
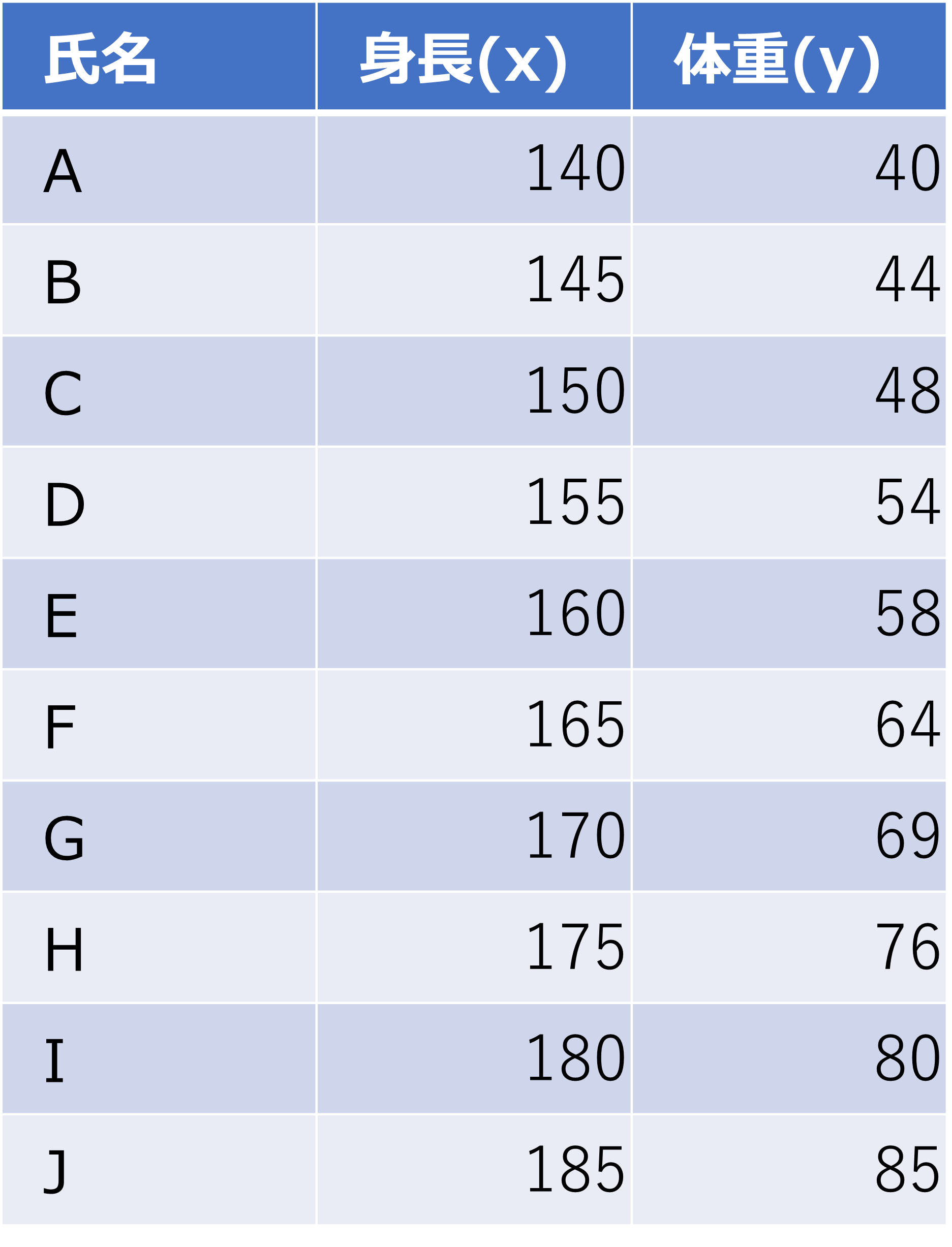
<単回帰分析>
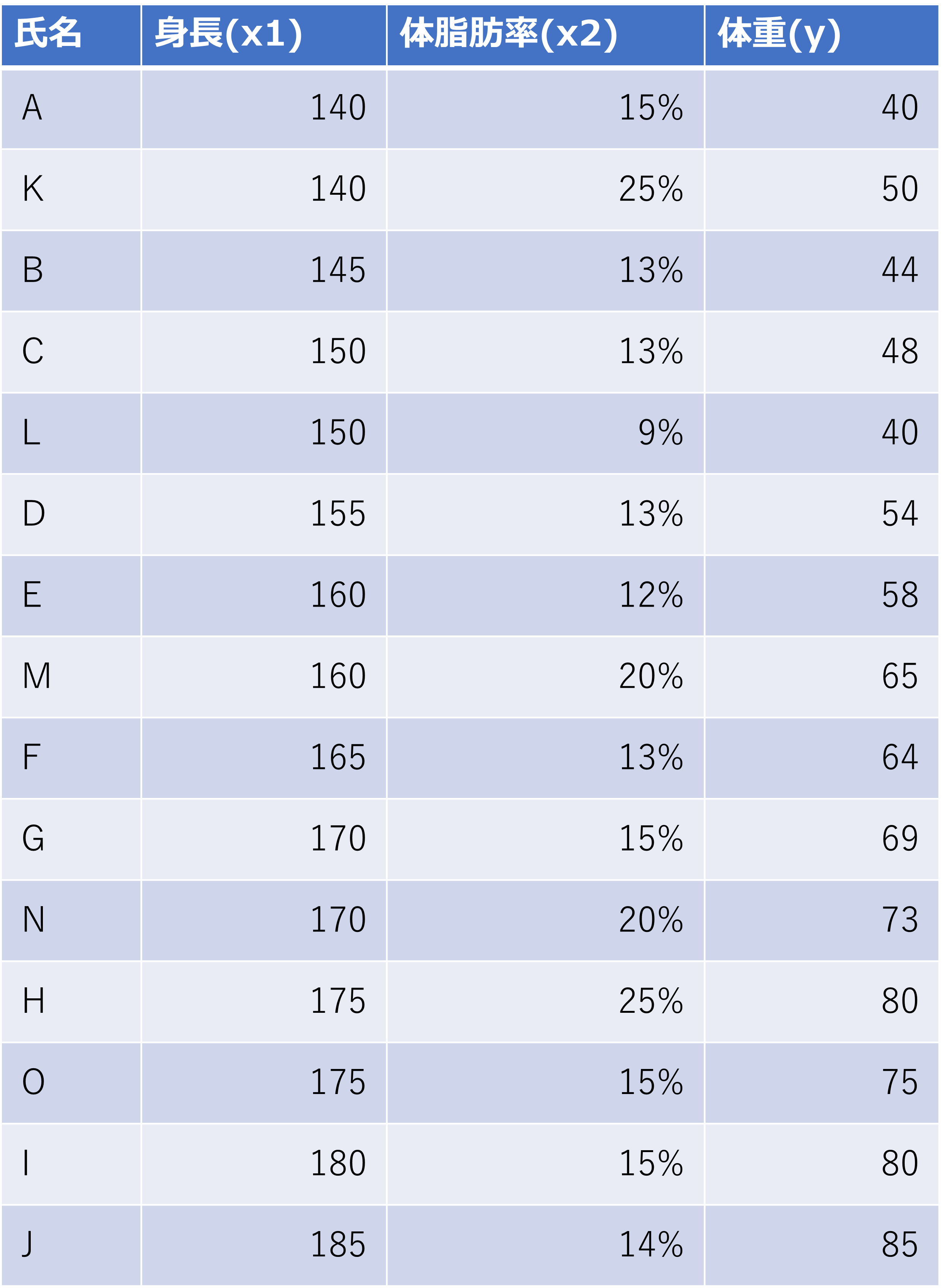
例:10 人の被験者の身長と体重のデータ。
・身長が5cm伸びたときに体重は約5kg重くなっている
・y= ax+bの数式に表すことで身長と体重の間にある関係を表現できる
<重回帰分析>
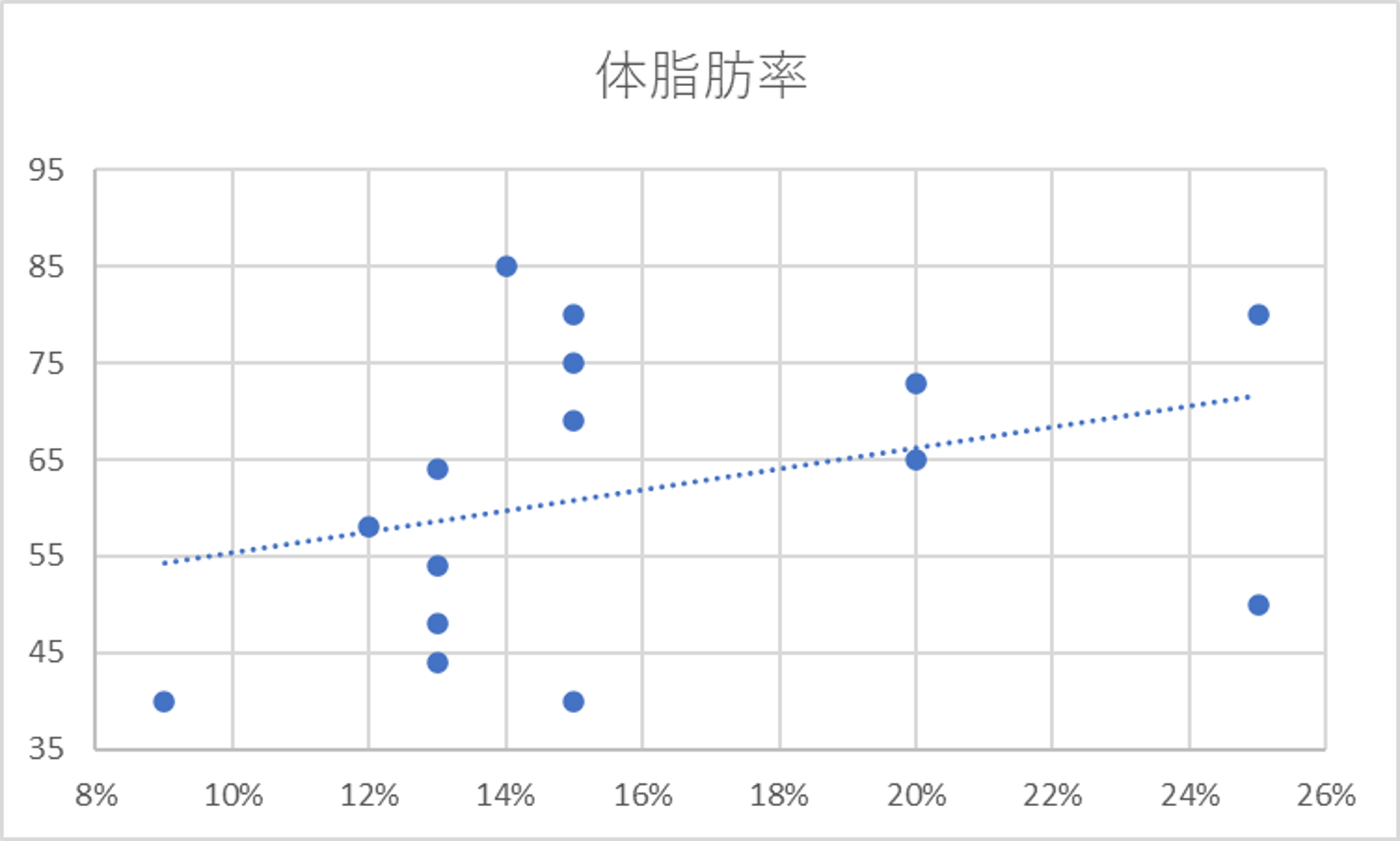
単回帰の例にさらに5人追加した被験者の身長と体脂肪率と体重のデータ 。
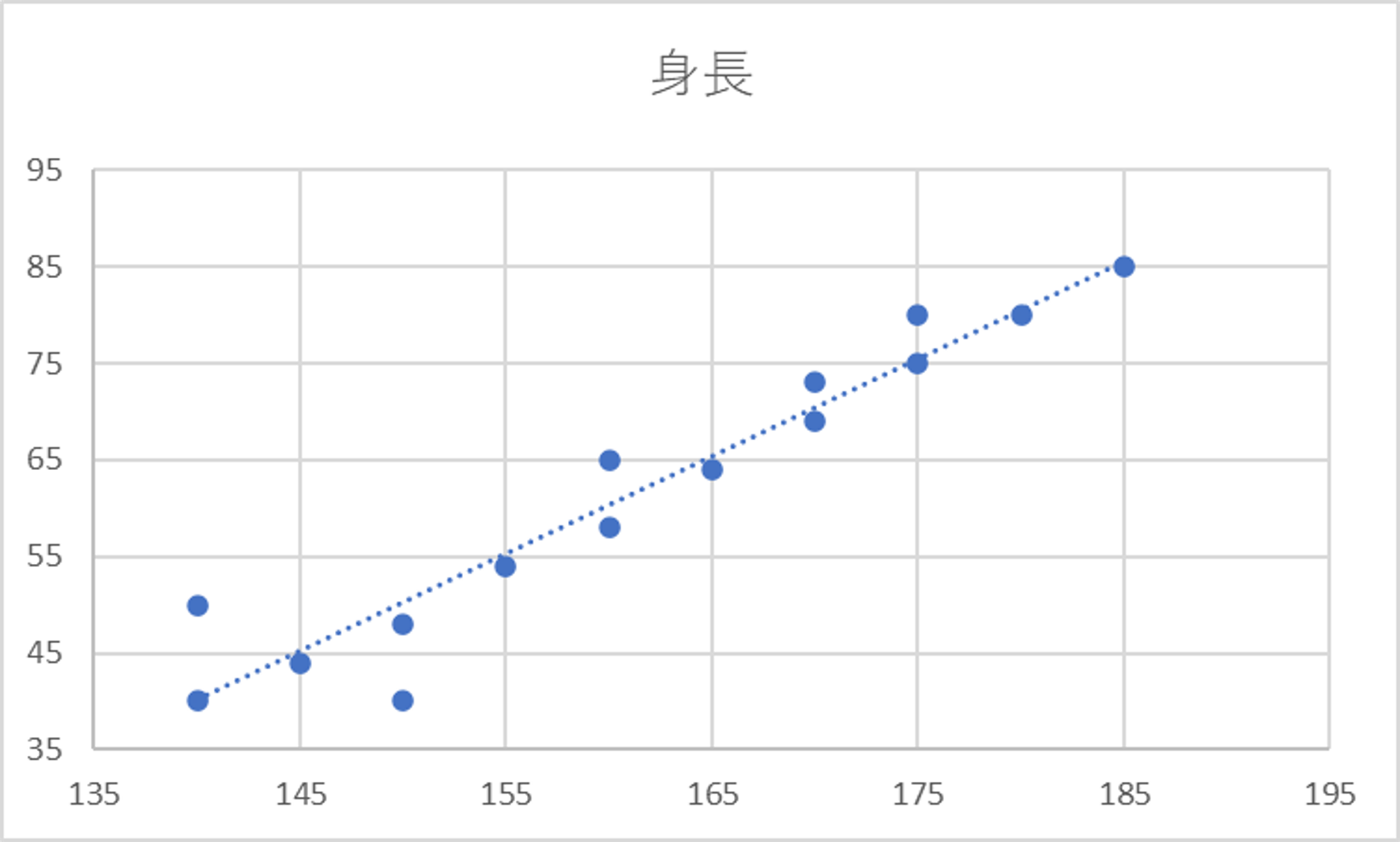
・身長と体重の関係をみると被験者が増えたことでばらつきが大きくなっており単回帰の式では関係を表現しきれない。
・体脂肪率と体重との関係をみるとばらつきが大きい
・身長と組み合わせることで体重の増減との関係が説明できそうである。
→(直感的にも身長が高く、体脂肪率も高ければ体重は増加する。その逆も然りというのはイメージしやすい)
・y=b1x1+b2x2+…b0の形で式に表すことで3つの指標の間にある関係を表現できる。この時のb1,b2は標準化係数(※) x1,x2は説明変数
※標準化係数
影響を与える大きさを表しており、身長(cm)、体脂肪率(%)のように桁数や単位が違くても比較できるようにするための係数。これにより単位を意識することなく関係を学習している。Geminiotの回帰で採用されているすべてのアルゴリズムでこのような変換をおこなっている。
1-3. 時系列分析の学習のイメージ
<時系列分析>
とある小売店の過去2年の売り上げデータ
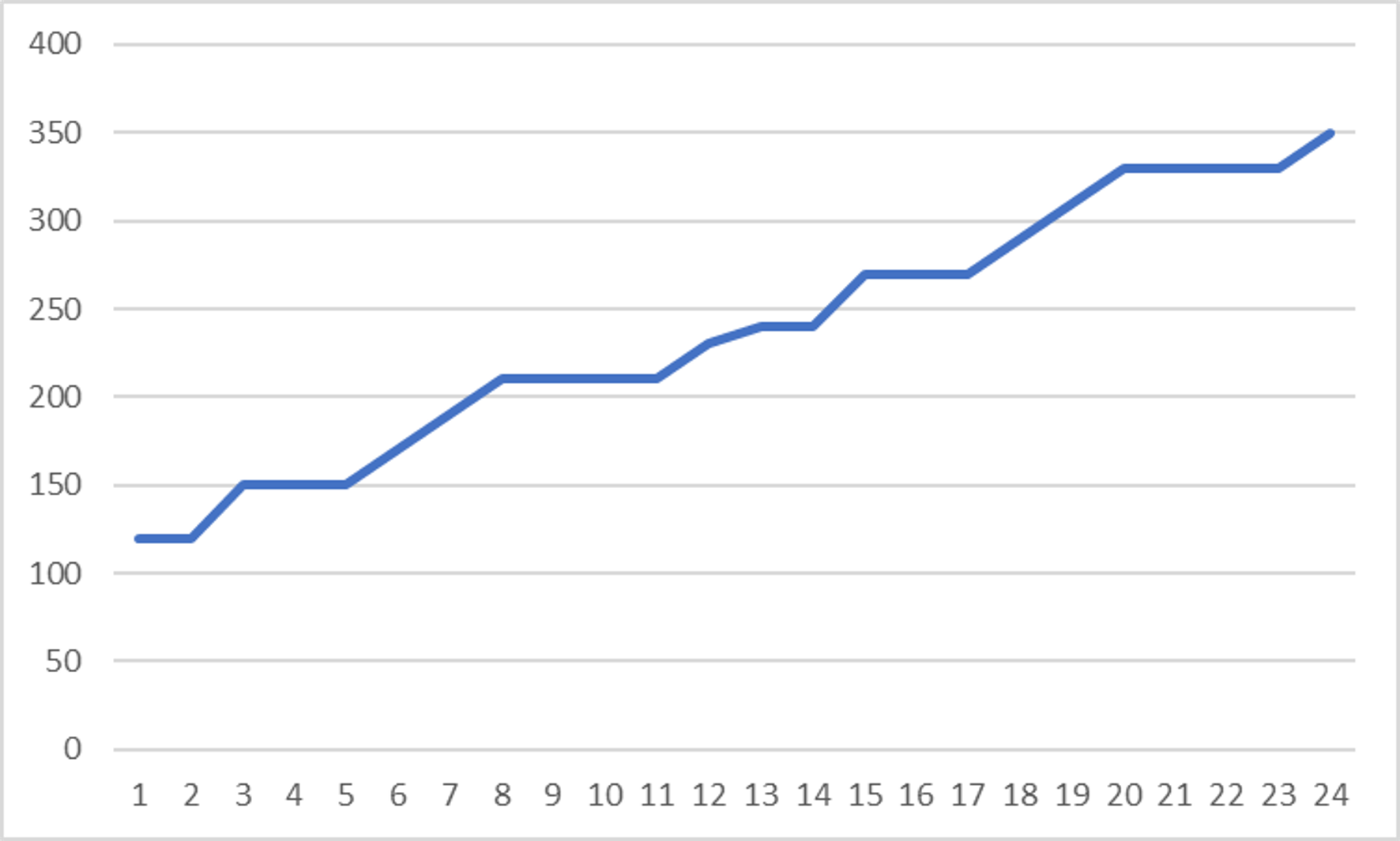
過去から現在までの売り上げを時系列に並べると上のようなグラフとなる

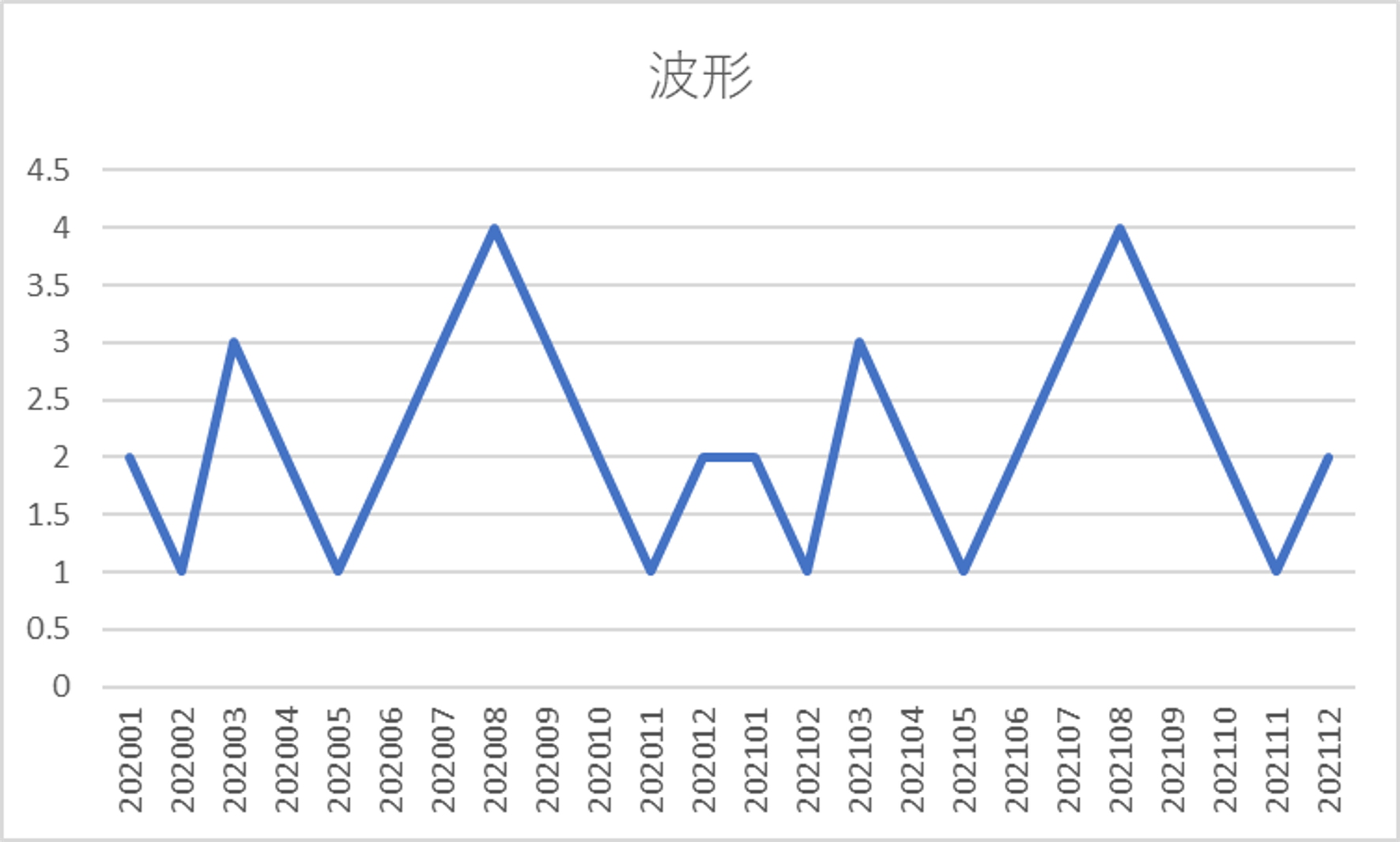
波形:時系列の売り上げから増減の情報だけ取り出す
→ 一定周期で増減を繰り返していることがわかる
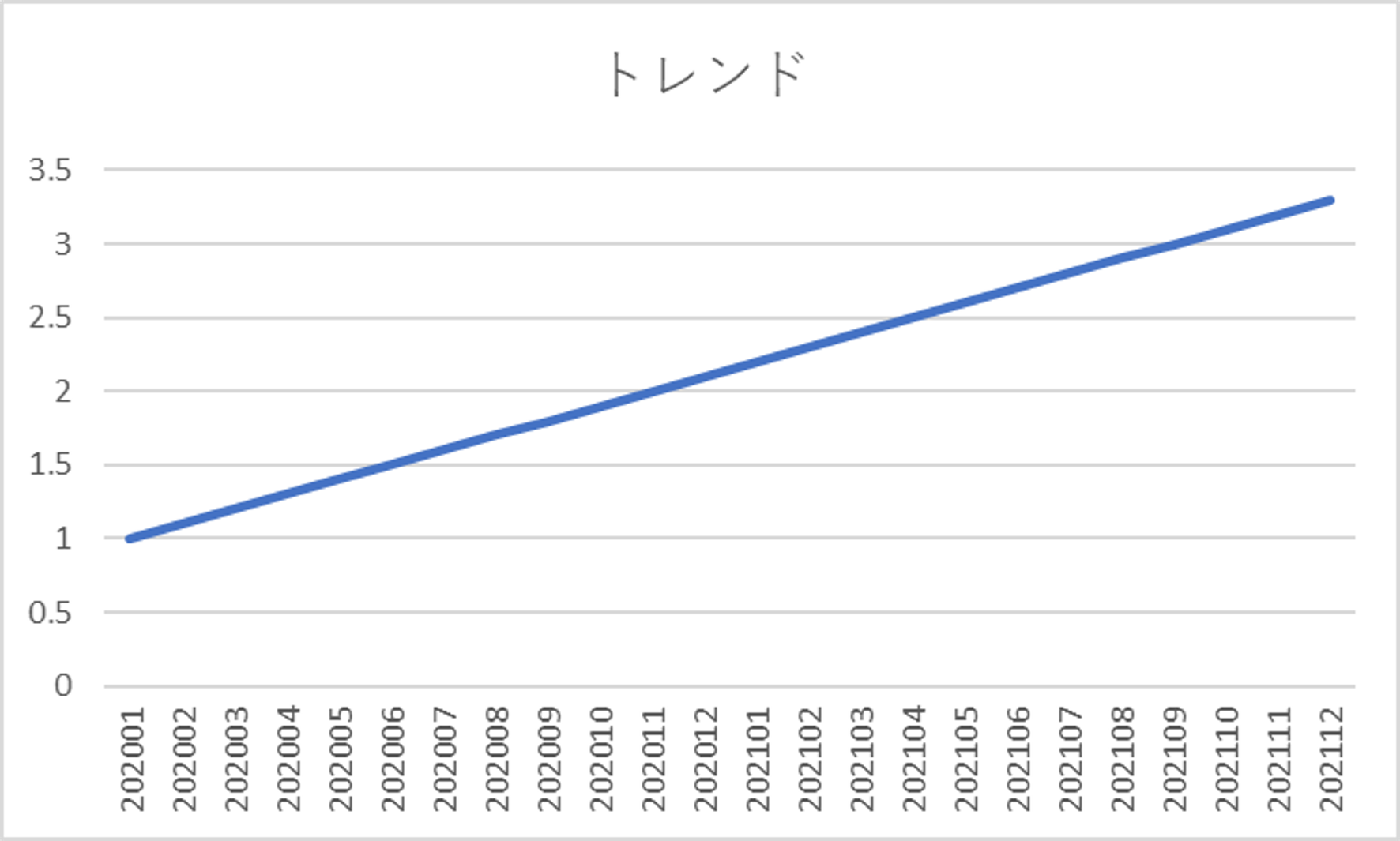
トレンド:時系列の売り上げから上昇傾向なのか下降傾向なのかの情報を取り出す(トレンド)
→ 右肩上がりになっている
以上の2つの情報を踏まえて将来の売り上げを予測することができる。
Geminiot の回帰分析で基本となるデータの形式
前提として学習や予測値の算出は各レコードごとに実施されます。
そのため、目的変数とそれに影響を及ぼす指標(説明変数)は各レコード毎に参照できる状態になっていることが基本となります。
<適した形>
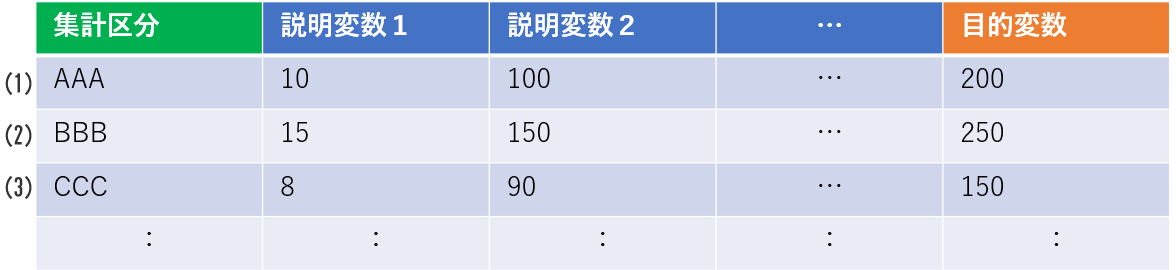
(1) 説明変数1の値は10、説明変数2の値は100…この時の目的変数の値は200
(2) 説明変数1の値は15、説明変数2の値は150…この時の目的変数の値は250
(3) 説明変数1の値は8、説明変数2の値は90…この時の目的変数の値は150
<適さない形>
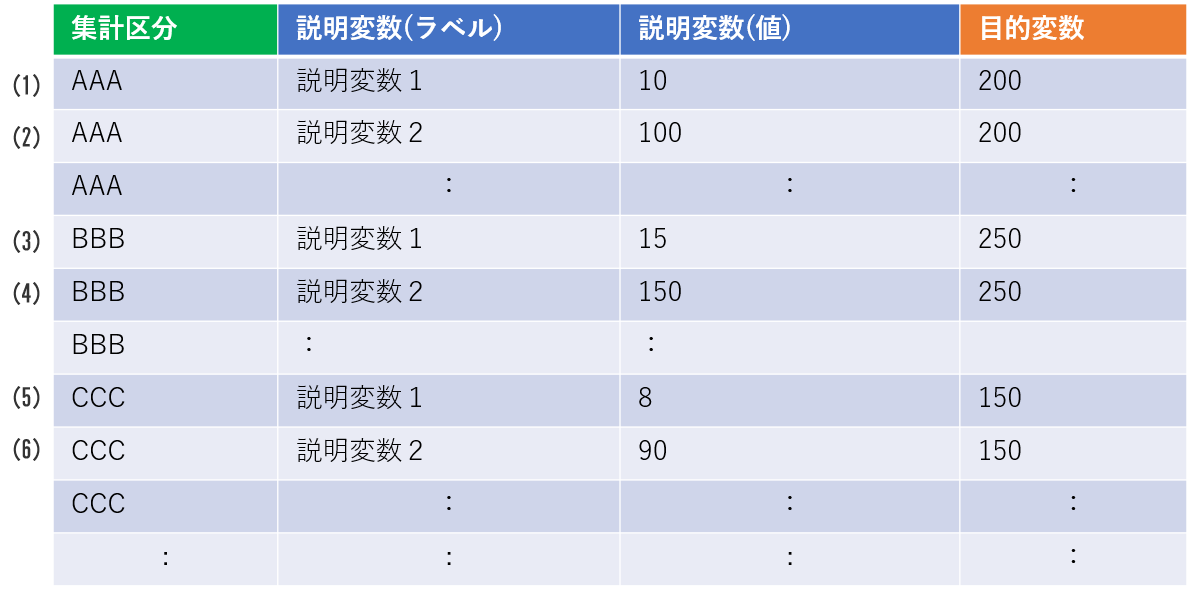
(1) 説明変数1の値は10、この時の目的変数の値は200
(2) 説明変数2の値は100、この時の目的変数の値は200
(3) 説明変数1の値は15、この時の目的変数の値は250
(4) 説明変数2の値は150、この時の目的変数の値は250
(5) 説明変数1の値は8、この時の目的変数の値は150
(6) 説明変数2の値は90、この時の目的変数の値は150
※説明変数1と目的変数の関係を表すレコードと、説明変数2と目的変数の関係を表すレコードが混在。
レコード毎に予測を行うため、複数の変数を加味した学習ができない。
周期性の反映について
周期性とは、一定毎に繰り返される変動パターンのことです。
時系列順にデータを保有している場合、季節波動や業務特性などによって何らかの周期性があることが考えられます。
周期性のあるデータで回帰分析を行う場合、意味のある情報として取り込んでおきたい指標となり得ます。
ただし、回帰予測ではレコード単位の計算となりますので、縦に時系列が連なった状態では周期性をうまく取り込むことができません。
周期性を反映するためにはデータを加工する必要があります。
※以下、例)年月ごとの売上を表している「時系列順に縦に連なったデータ」があります。同じ月ごとに売上を、横に並べることで当年と昨年の売上として比較できるようになり周期性が反映されます(「当年と昨年の売り上げを横に並べたデータ」)。
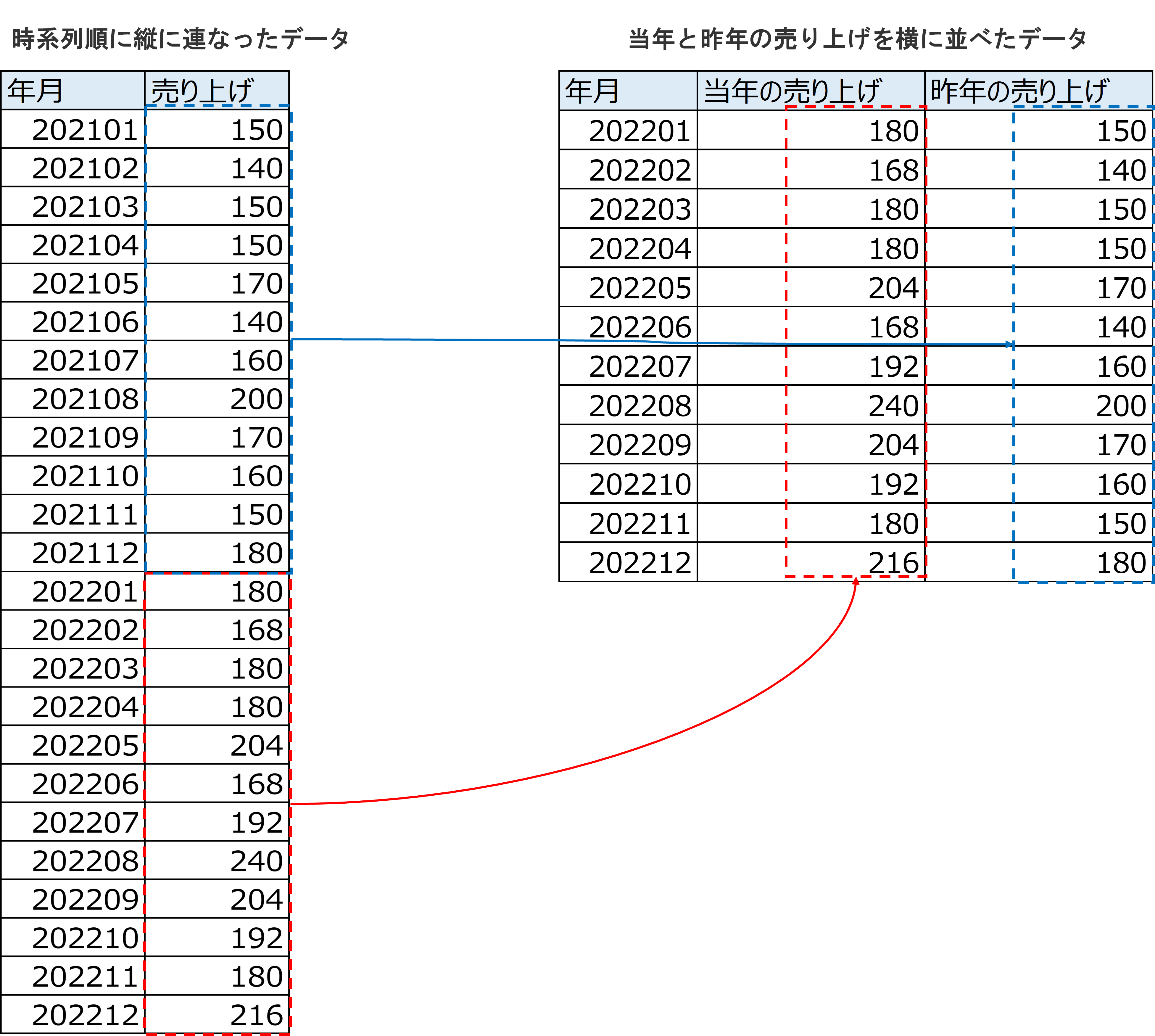
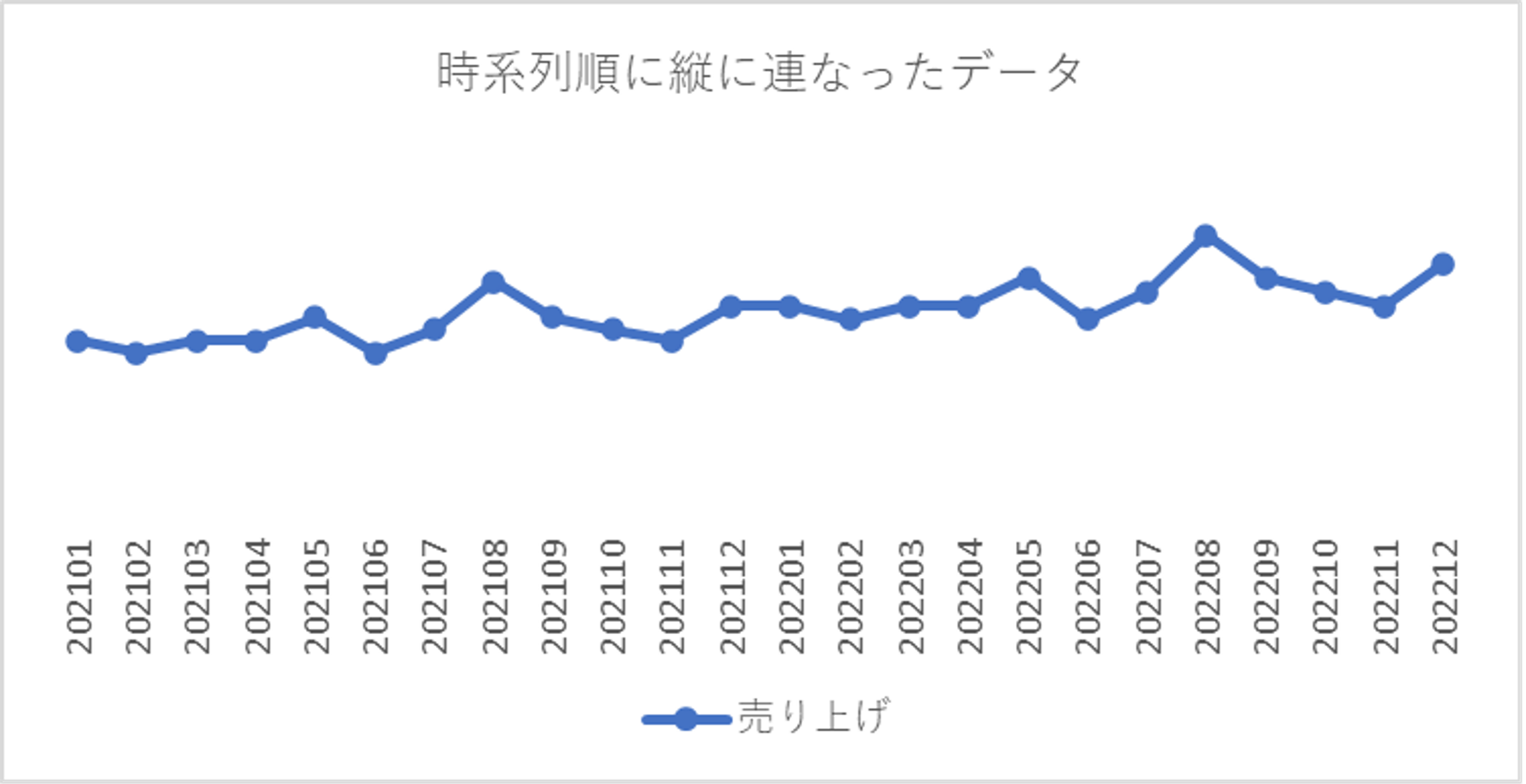
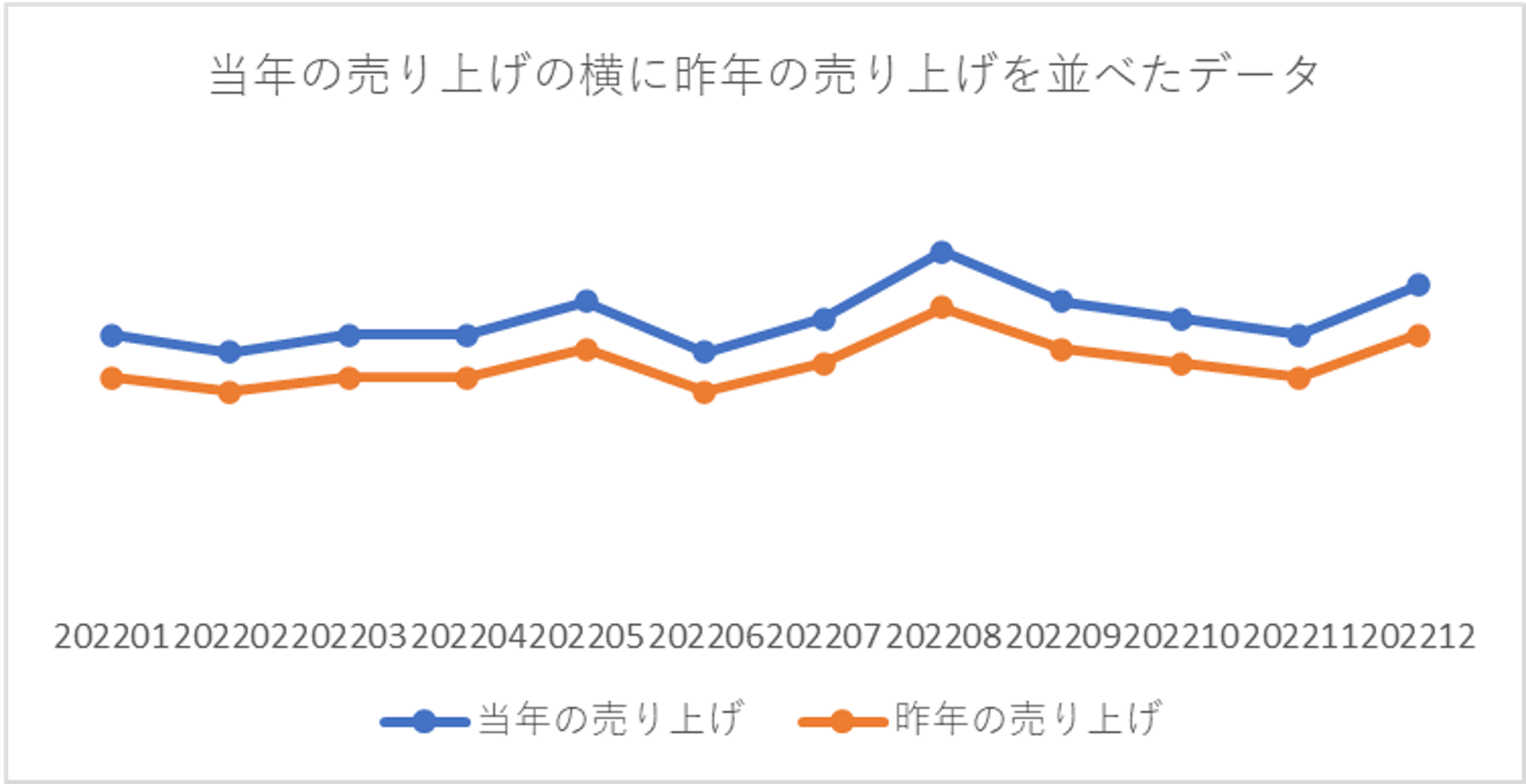
昨年の売り上げで当年の売り上げを説明できそう。
Geminiot/Pasterio.miで気軽にデータ分析
以上のような回帰分析に適した形のデータで分析を行えば、思うような予測結果が得られるのではないでしょうか。
ところで皆さんは、データ分析は何で行いますか?データ分析はExcelでも行うことは可能です。
しかし、より素早く簡単にデータ分析を行うなら、データ分析専用ツールを利用するのがおすすめです。
データ分析ツールは様々ありますが、「Geminiot/Pasterio.mi」であれば、月々4万円~という低価格でデータの分析・活用を行うことが出来ます。
Geminiot/Pasterio.miはデータの可視化に留まらず、AIを活用してインサイト(気づき)を導き出し業務の改善につなげる一歩踏み込んだ製品です。
デジタルツイン(=現実世界をデジタル空間上に再現する)機能を搭載し、業務フローとKPI、それに紐づくデータを設定することで、AI分析モデルやKPIに対する予測結果、影響を及ぼす要因が記載された分析結果のダッシュボードを自動生成します。
そこから得られる気づきに対して現実世界で対策を行うことで、業務の改善を行うことができます。
またデータ分析・活用に必要な、データの収集加工、AIモデルの開発、ダッシュボード開発、それぞれの機能を全て搭載しています。
Geminiot/Pasterio.miひとつで、データ収集・加工・分析・可視化をすることができ、インサイトが得られ、効果的なデータ活用を行うことができます。
初期費用0円!ユーザー登録ですぐにご利用いただけます。


